Tema 5: Energía, Leyes Físicas y Razonamiento Mecánico
En esta unidad aprenderemos:
El vehículo como maquina mecánica, produce energía de movimiento que implica una serie de principios que deben ser dominados no solo por los especialistas mecánicos, sino que también por los instructores de manejo. Por ello, en este módulo comprenderemos el impacto las fueras de movimiento producidas a través de la mecánica del vehículo, aplicadas a la conducción y sus múltiples variables.
Energía y las leyes físicas
Energía y movimiento
Los objetos transportados están sometidos a una serie de fuerzas que exigen su adecuada sujeción para evitar los desplazamientos en el interior del vehículo con grave riesgo de accidente. Estas fuerzas son, fundamentalmente: Fuerza de Inercia y Fuerza Centrífuga.
Fuerza de Inercia
Si no se aplicara ninguna fuerza, un vehículo que está en reposo, continua en reposo, y si un vehículo está en movimiento, continua moviéndose indefinidamente. Este principio sólo funciona en el plano teórico. En la realidad no existe así. Sobre un vehículo en movimiento actúan diferentes fuerzas que se oponen: resistencia del aire, rozamiento de las ruedas, etc. Además, actúan otras fuerzas como la aceleración (variación de la velocidad de un cuerpo en función del tiempo), que puede ser negativa (frenadas, desaceleraciones) o positiva (aceleraciones):
- En aceleraciones negativas: la carga o los pasajeros tienden a mantener la misma velocidad que el vehículo y a desplazarse hacia la parte delantera.
- En aceleraciones positivas: la carga o los pasajeros tienden a desplazarse hacia la parte trasera del vehículo, aunque con menor fuerza inercial que en el caso anterior.
¿Qué provoca la fuerza de inercia?
La fuerza de inercia provoca que un vehículo acercándose a una curva mantenga una trayectoria en línea recta. A través del volante usted puede controlar la dirección, sin embargo, a altas velocidades esto se complica y podría perder fricción saliéndose de la vía.
Siempre recuerde al conducir:
- Verificar con anticipación el estado del camino.
- Estar atento a cualquier sorpresa mientras conduce.
- Las hojas caídas, derrames de combustible, pérdidas de aceite, provocan que el pavimento sea resbaladizo.
- Baje la velocidad con anticipación antes de la curva y acelere suave a la salida de la curva.
- La fuerza centrífuga en una curva tiende a sacar al automóvil de la vía dependiendo de la velocidad y de lo cerrada que sea la curva.
Fuerza Centrífuga
Es la que tiende a sacar la carga o los ocupantes del vehículo hacia el exterior cuando el vehículo toma una curva, efectúa un cambio de dirección o da un giro brusco del volante.
Movimientos longitudinales y laterales del vehículo
Es necesario conocer el comportamiento físico del vehículo y las fuerzas que actúan sobre él en las diferentes situaciones que se producen durante la conducción.
Estas fuerzas, sobre las que los conductores intervienen de forma directa, son:
- La fuerza de empuje.
- La fuerza de frenado.
- La de guiado lateral (fuerza centrípeta).
- La adherencia.
En la conducción también están otras fuerzas presentes, como son:
- La resistencia del aire.
- El par de rueda y de inercia.
- Los pares de viraje (derrape).
Energía Cinética
El vehículo y su carga, están sujetos a las leyes de la física, en especial a la energía cinética, que acumulan los objetos y las personas en un vehículo en movimiento.
Los objetos mal sujetos pueden desplazarse con una fuerza excepcional y provocar daños en los ocupantes, en el vehículo o a terceros.
Cuando aceleramos subiendo una pendiente, la carga tiende a desplazarse hacia la parte trasera; por el contrario, en una pendiente descendente, si hay que hacer una fuerte frenada, la carga tiende a desplazarse hacia la parte delantera.
En una frenada de emergencia algunos objetos cotidianos pueden ser realmente peligrosos, por efectos del desplazamiento de la energía cinética, para comprender tal magnitud podemos analizar la multiplicación de la masa:
| Objeto | Peso real | Peso en caso de impacto |
| Celular | 110 g | 6,2 kg |
| Paraguas | 440 g | 25 kg |
| Libro | 2 kg | 113 kg |
| Mochila | 5 kg | 283 kg |
| Paquete | 25 kg | 1.417 kg |
Distancia de Reacción
En un vehículo, el velocímetro nos informa sobre la relación de dos variables “distancia” y “tiempo”, por ello estas medidas se expresan de la siguiente forma 50km/hr, es decir, el vehículo va a una velocidad que le permitirá recorrer una distancia de 50 kilómetros en una hora.
Por otra parte, los frenos en un vehículo son el elemento central de la Seguridad Activa pues evitan accidentes. (La Seguridad Pasiva minimiza las consecuencias de un accidente, como el cinturón de seguridad o el apoyacabeza).
Al momento de decidir frenar, todos los conductores deben estar conscientes de la distancia estimada que recorrerá su vehículo mientras reaccionan.
¿Qué es la Distancia de Reacción?
Definición
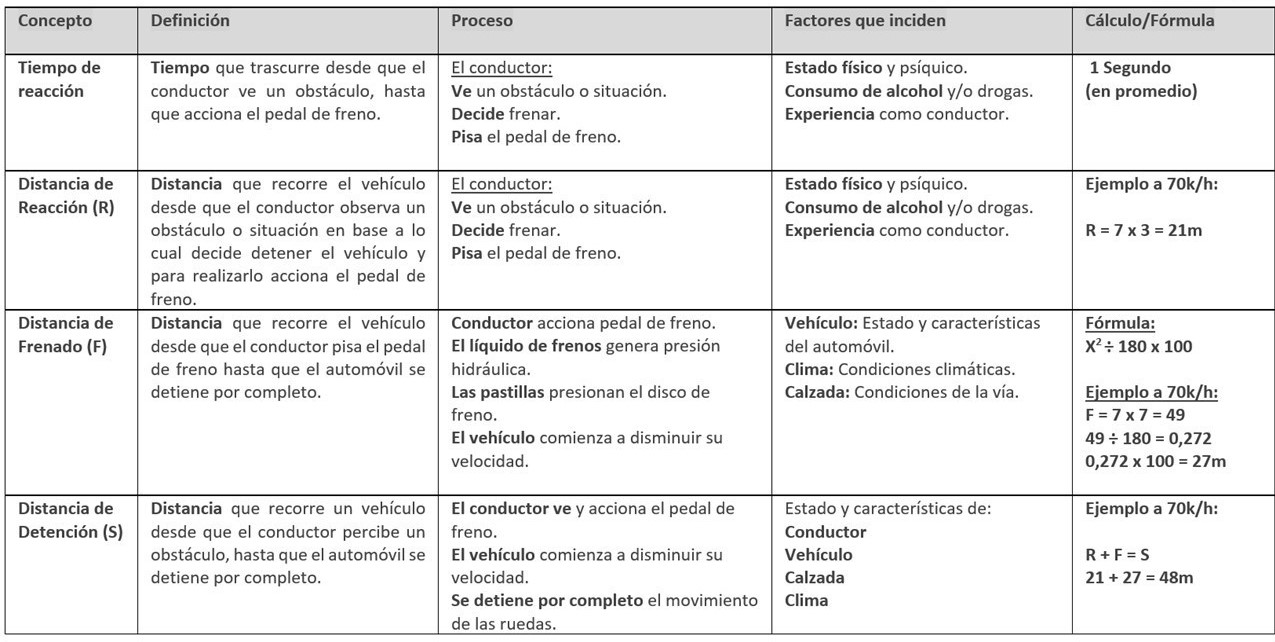
Es la distancia que recupera el vehículo desde que el conductor observa un obstáculo o situación en base a lo cual decide detener el vehículo y para realizarlo pisar el pedal de freno.
Proceso
El conductor:
1 – Percibe peligro, obstáculo o situación.
2 – Saca pie del acelerador (desaceleración)
3 – Presiona pedal de freno.
Se estima que este proceso toma en promedio 1 segundo y es esta referencia que se utiliza para el cálculo estandarizado de la distancia de reacción.
Factores que influyen en la Distancia de reacción:
Múltiples factores influirán en la distancia real de reacción en cada situación, centrados principalmente en el conductor, como:
- Estado físico y psíquico. (Ej: fatiga, sueño y somnolencia).
- Consumo de alcohol y/o drogas.
- Experiencia como conductor.
¿Cómo se calcula la Distancia de Reacción?
Es posible realizar el cálculo de varias formas, te presentamos dos métodos muy simples.
Método 1: Cálculo Distancia de Reacción “Multiplicar por 3”
De forma estandarizada y promediada, se estima que un conductor experimentado demora 1 segundo en reaccionar para frenar, por ello es posible multiplicar por 3 el primer dígito de la velocidad del vehículo para obtener, en medida de metros recorridos, la Distancia de Reacción.
Ejemplos de método 1:
- Un vehículo se desplaza a 90 km/h
Cálculo: 9 x 3 = 27m.
La Distancia de Reacción recorrida por un vehículo que se desplaza a 90 km/h es de 27 metros aproximadamente.
- Un vehículo se desplaza a 50 km/h
Cálculo: 5 x 3 = 15m.
La Distancia de Reacción recorrida por un vehículo que se desplaza a 50 km/h es de 15 metros aproximadamente.
Método 2: Cálculo Distancia de Reacción “Dividir por 3,6”
A pesar de que este método da un resultado más exacto, es difícil utilizarlo de forma mental al rendir el examen teórico de conducción. Consiste en calcular la distancia recorrida por un vehículo en un segundo. Para ello, se debe dividir la velocidad por 3,6.
Ejemplos de método 2:
1. Un vehículo se desplaza a 85 km/h
Cálculo: 85 ÷ 3,6 = 23,6m.
La Distancia de Reacción recorrida por un vehículo que se desplaza a 85 km/h es de 23,6 metros aproximadamente.
2. Un vehículo se desplaza a 40 km/h
Cálculo: 40 ÷ 3,6 = 11,1m.
La Distancia de Reacción recorrida por un vehículo que se desplaza a 40 km/h es de 11,1 metros aproximadamente.
¿Qué distancia recorre un vehículo en un segundo?
Para comprender el fundamento de los cálculos que se realizan para estimar la Distancia de Reacción, te recomendamos descubrir en la siguiente ficha ¿Qué distancia recorrerá un vehículo en una hora, un minuto y un segundo si se desplaza, por ejemplo a 70km/h?:

Entonces podemos inferir que un vehículo que se desplaza a 70 km/h recorre una distancia aproximada de 19 metros por segundo.
Distancia de Frenado
Luego de la Distancia de Reacción, que es la que recorre un vehículo tras la activación del sistema de frenos por parte del conductor, todos los elementos de dicho sistema se ponen en funcionamiento en el automóvil hasta que las ruedas dejan de girar y se logra la detención total. Esta distancia recorrida por el vehículo se denomina Distancia de Frenado. Entonces podemos decir que “el conductor reacciona” y “el vehículo frena” tras la activación del sistema por parte del conductor.
¿Qué es la Distancia de Frenado?
Definición
Es la distancia que recorre el vehículo desde que el conductor pisa el pedal de freno hasta que el automóvil se detiene por completo.
Proceso
- Conductor acciona pedal de freno.
- El liquido de frenos genera presión hidráulica.
- Las pastillas presionan el disco de freno.
- El vehículo comienza a disminuir su velocidad.
Factores
Los múltiples factores que inciden en la Distancia de Frenado se pueden clasificar en tres grandes grupos:
- Vehículo: Estado y características del automóvil.
- Clima: Condiciones.
- Calzada: Condiciones de la vía.
¿Cómo se calcula la Distancia de Frenado?
Es posible realizar el cálculo de varias formas, te presentamos los dos métodos muy comunes, en orden de dificultad.
Método 1: Cálculo Distancia de Frenado “Multiplicar por 5”
La forma aproximada más simple para calcular la Distancia de Frenado de forma mental el día del examen teórico de conducción es multiplicar la primera cifra de la velocidad por 5.
Ejemplo método 1:
1. Un vehículo se desplaza a 90 km/h
Cálculo: 9 x 5 = 45m.
La Distancia de Frenado recorrida por un vehículo que se desplaza a 90 km/h es de 45 metros aproximadamente.
Método 2: Cálculo Distancia de Frenado “Primer digito al cuadrado, dividir por 180 y multiplicar por 100”
Este método es más complejo y tal vez difícil para utilizar el día del examen teórico de conducción, pero puede ser más exacto. Consiste en elevar el primer dígito de la velocidad al cuadrado, dividir por 180 y luego multiplicar el resultado por 100.
Ejemplo método 2:
1. Un vehículo se desplaza a 70 km/h
Cálculo: 7 x 7 = 49 ÷ 180 = 0,272 x 100 = 27
La Distancia de Frenado recorrida por un vehículo que se desplaza a 70 km/h es de 27 metros aproximadamente.
Distancia de Detención
A mayor velocidad el vehículo recorre mayor distancia para detenerse por completo en caso de que el conductor requiera frenar, especialmente cuando debe realizarlo por alguna emergencia. Por ello, es indispensable para todos los conductores comprender sepan realizar cálculos y/o estimaciones sobre la Distancia de Detención.
¿Qué es la Distancia de Detención?
Definición
La Distancia de Detención es el trecho que recorre un vehículo desde que el conductor percibe un obstáculo, hasta que el automóvil se detiene por completo. Este proceso se divide en Distancia de Reacción y Distancia de Frenado:
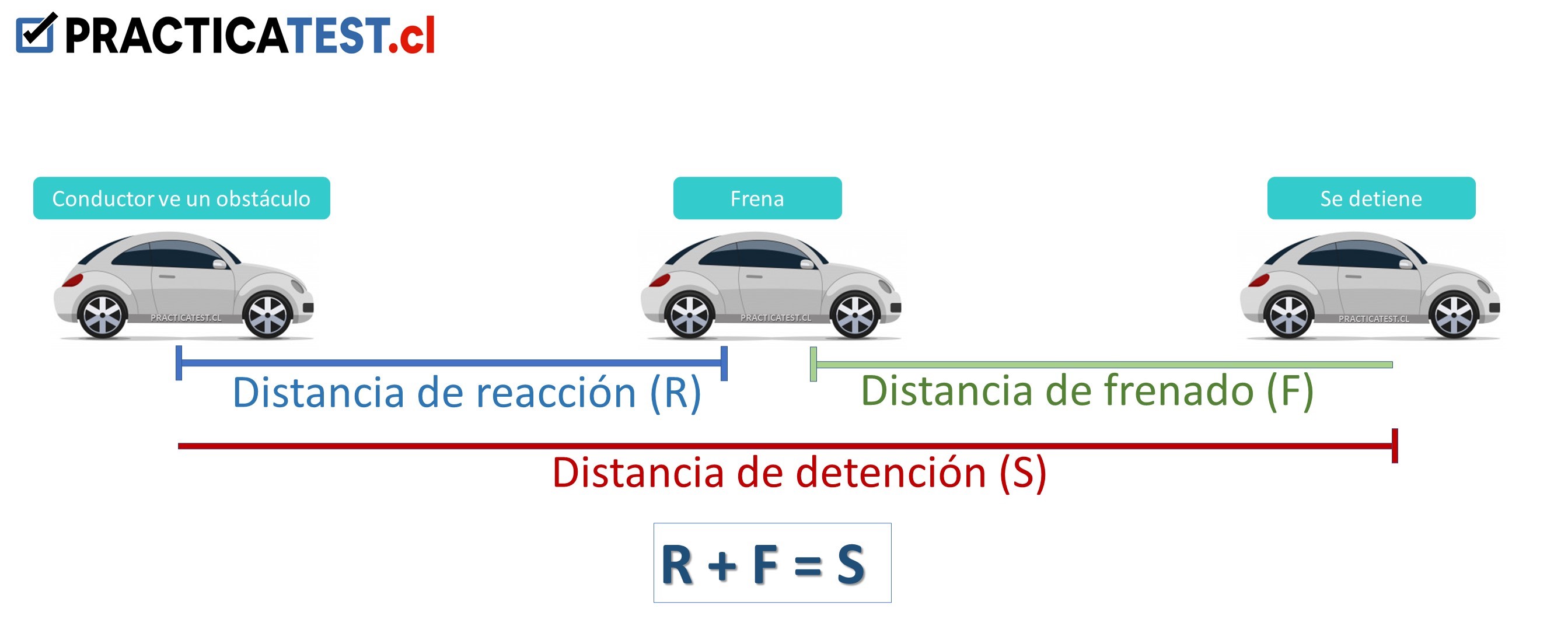
Conceptos
¿Cómo se calcula la Distancia de Detención?
La Distancia de Detención Total de un vehículo es la suma de la Distancia de Reacción más la Distancia de Frenado , por ello el ejercicio consiste en calcular ambas distancias por separado y luego sumarlas. Para lograrlo existen varias opciones a continuación, te presentamos dos una simplificada y aproximada y otra más compleja pero más exacta.
Método 1: Cálculo Distancia de Detención “Multiplicar por 3 y por 5”
La forma aproximada más simple para calcular la Distancia de Detención de forma mental el día del examen teórico de conducción, según el Libro del Nuevo Conductor de Conaset es:
Distancia de reacción: Multiplicar la primera cifra de velocidad por 3.
Distancia de Frenado: Multiplicar la primera cifra de velocidad por 5.
Distancia de Detención: Sumar Distancia de Reacción más Distancia de Frenado.
Ejemplos de método 1:
Un vehículo se desplaza a 70 km/h
Cálculo Distancia de Reacción: 7 x 3 = 21m
La Distancia de Reacción recorrida por un vehículo que se desplaza a 90 km/h es de 21 metros aproximadamente.
Cálculo Distancia de Frenado: 7 x 5 = 35m
La Distancia de Frenado recorrida por un vehículo que se desplaza a 90 km/h es de 35 metros aproximadamente.
Cálculo Distancia de Detención: 21 + 35 = 56m
La Distancia de Detención recorrida por un vehículo que se desplaza a 90 km/h es de 56 metros aproximadamente.
Método 2: Cálculo Distancia de Detención
Distancia Reacción = “V ÷ 3,6” o “X x 2,77”
Distancia Frenado = “X² ÷ 180 x 100”
Distancia de Detención: Sumar Distancia de Reacción más Distancia de Frenado.
Importante:
En las fórmulas la variable incógnita “V” corresponde a la velocidad del vehículo, entonces V = Velocidad.
En las fórmulas la variable incógnita “X” corresponde al primer dígito de la velocidad del vehículo.
Ejemplos de método 2:
Un vehículo se desplaza a 70 km/h
Cálculo Distancia de Reacción:
Opción 1 “dividir”: 70 ÷ 3,6 = 19,4m
Opción 2 “multiplicar”: 7 x 2,77 = 19,39m
La Distancia de Reacción recorrida por un vehículo que se desplaza a 70 km/h es de 19 metros aproximadamente.
Cálculo Distancia de Frenado:
7 x 7 = 49 ÷ 180 = 0,272 x 100 = 27,2
La Distancia de Frenado recorrida por un vehículo que se desplaza a 70 km/h es de 27 metros aproximadamente.
Cálculo Distancia de Detención:
19 + 27 = 72m
La Distancia de Detención recorrida por un vehículo que se desplaza a 70 km/h es de 46 metros aproximadamente.
¿Por qué 3,6?
La razón de utilizar la cifra 3,6 como “factor de conversión” se basa en que 1 hora equivale a 3.600 segundos, entonces al saber la distancia que recorrerá el vehículo en 1 hora, por ejemplo “70km/h” podemos calcular que distancia recorrerá en 1 segundo a la misma velocidad dividiendo la velocidad por 3,6.
Recordemos que se estima que en promedio un conductor demora 1 segundo en reaccionar para frenar.
Cálculo:
1 hora = 60 minutos
1 Minuto = 60 segundos
Entonces:
60x60 = 3.600
1 Hora = 3.600 segundos
Es así como:
Un vehículo a 70km/h registra 70 kilómetros en 3.600 segundos
Equivalencia de distancia:
1 Kilómetro = 1.000 metros
por ello
70 Kilómetros = 70.000 metros
Simplificación por 1.000:
La simplificación consiste en dividir ambas cifras por el mismo número manteniendo la equivalencia de la expresión, en este caso “100”, entonces:
70.000 / 1.000 = 70
3.600 / 1.000 = 3,6
Esto explica como:
70.000 ÷ 3.600 = 70 ÷ 3,6
Entonces a 70k/h:
70 ÷ 3,6 = 19,4
¿Cómo convertir kilómetros por hora en metros por segundo?
La relación “kilómetros por hora” es completamente familiar para los conductores, que obviamente permite estimar cuántos kilómetros se recorrerán en una hora a velocidad constante, sin embargo existe otra medida equivalente denominada “metros por segundo”, por ello podemos estimar cuántos metros recorrerá el vehículo a velocidad constante convirtiendo km/h en m/s. Para ello expresaremos las variables y su relación en fracciones para luego realizar el cálculo matemático correspondiente.
Expresión de variables y medidas:
70 kilómetros por hora: 70 km/h
1 Hora equivale a 3.600 segundos: 1h/3.600s
1 kilómetro equivale a 1.000 metros: 1000m/1km
Entonces:
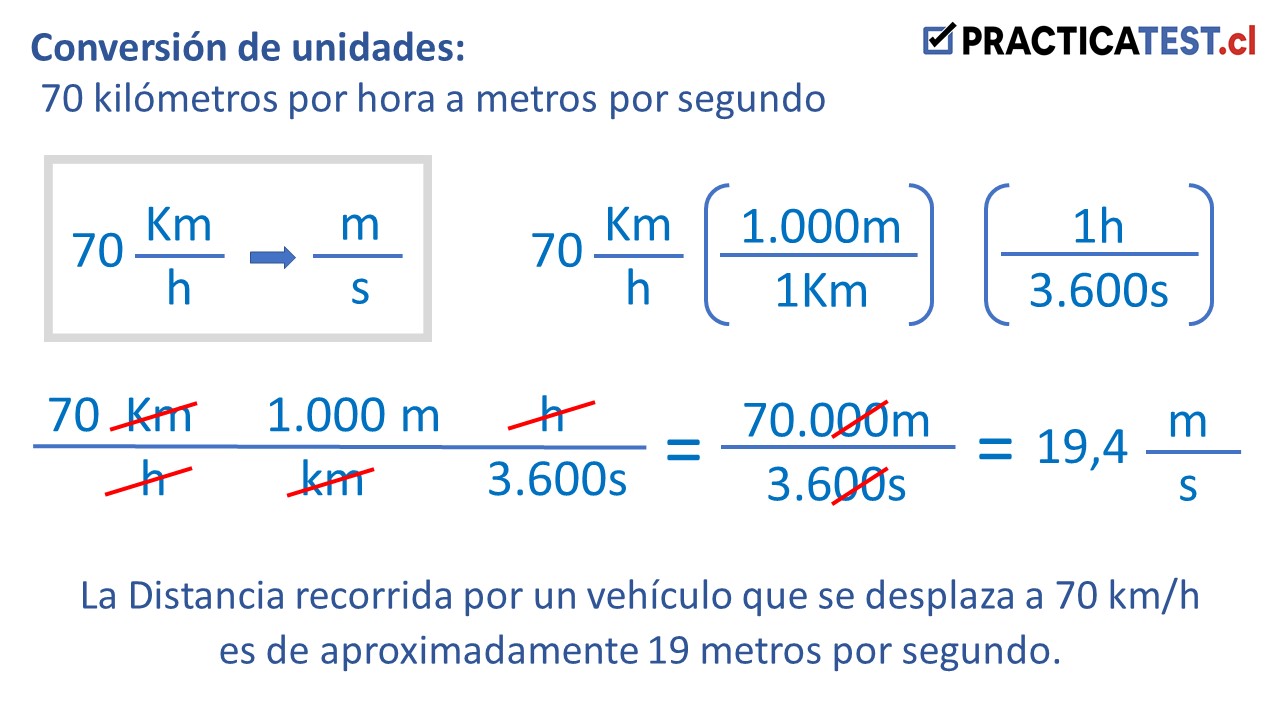
¿Por qué 2,77?
En Para determinar un “factor de conversión” aproximado en base al ejercicio anterior podemos realizar una simple ecuación de primer grado, que responde a:
¿Por qué cifra es posible multiplicar la velocidad en k/h para convertirla am/s?
Para un vehículo que se desplaza a 70k/h
Decimos que la primera cifra de la velocidad, en este caso 7, multiplicado por una incógnita X, da como resultado 19,4, entonces:
7xX = 19,4
X = 19,4 / 7
X = 2,77
¿Por qué se multiplica por 3 en la Distancia de Reacción?
Es una aproximación simplificada del 2,77 recién explicado.
Recordemos: ¿Qué distancia registra un vehículo en un minuto?
Para estimar la Distancia de Detención Total, que es la suma de Distancias de Reacción y Frenado, es necesario comprender que la velocidad (técnicamente es rapidez, pero no es problemático para estas explicaciones) de los vehículos se mide en “kilómetros por hora” (km/h) como indica el velocímetro y de ahí podemos deducir, calcular y/o determinar la misma relación en medidas de tiempo y distancia más pequeños como los metros recorridos por un vehículo en un segundo. Para ello, en la siguiente tabla respondemos a ¿Qué distancia registra un vehículo en una hora, un minuto y un segundo?:

Entonces un vehículo que circula a 70 km/h registra 19 metros por cada segundo. En términos físicos se “desplaza a 19 m/s”.
Razonamiento Mecánico
Definición:
El razonamiento mecánico es un proceso psicológico de orden superior a través del cual una persona puede identificar los componentes principales de un sistema mecánico y su relevancia para el funcionamiento del mismo e inferir cómo interactúan entre ellos. (Injoque-Ricle, I., Formoso, J., Calero, A., & Caruso, G., 2019)
Importancia:
Los principios y aplicación del razonamiento mecánico son fundamentales tanto en la mecánica automotriz como en la conducción, por ello instructores y nuevos conductores deben desarrollar las habilidades necesarias para resolver diversos problemas en el ámbito teórico y luego en la realidad en diversas situaciones como instructor y/o conductor.
Método:
La metodología de estudio para el Razonamiento Mecánico es situacional, es decir, se analizan casos y/o ejemplos puntuales de situaciones posibles con variables, de forma problemática para responder en general a preguntas cerradas, problemas dicotómicos como: ¿Cuál es la manera más práctica de cargar el saco en la carretilla?.
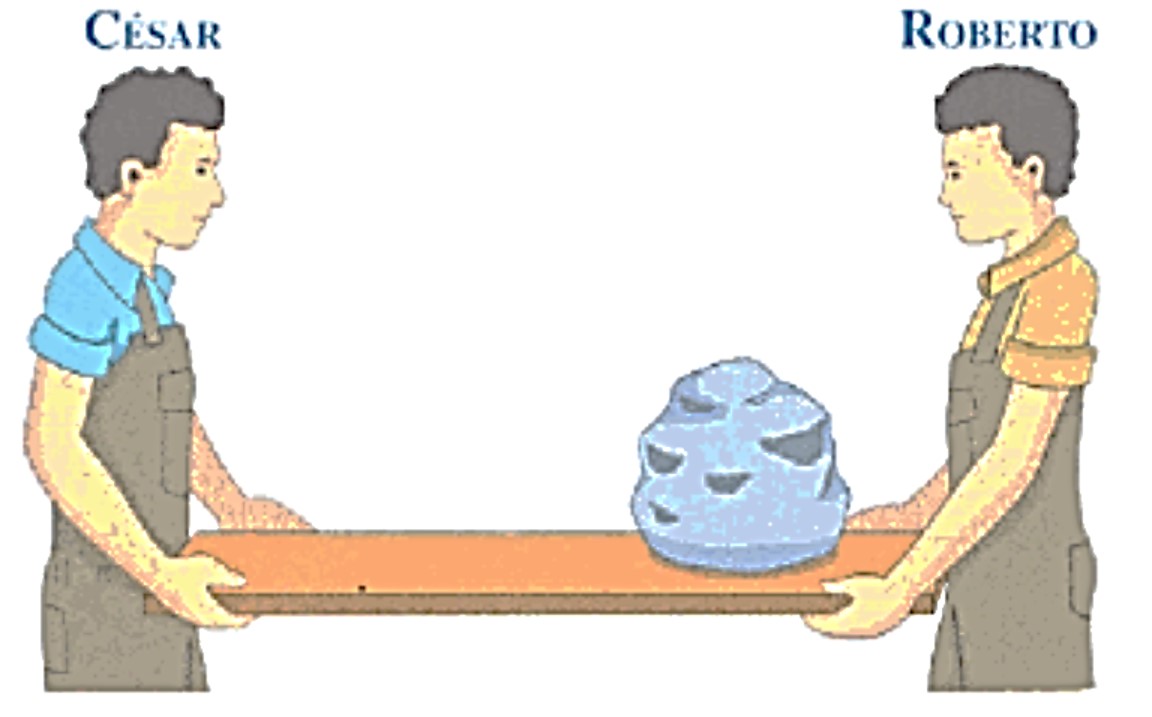
| Ejemplo:
¿Cuál de los amigos está soportando mayor peso? Razonamiento Mecánico: Al estar el objeto, que están sosteniendo ambos, más cerca de Roberto, él es quien está soportando mayor peso. |
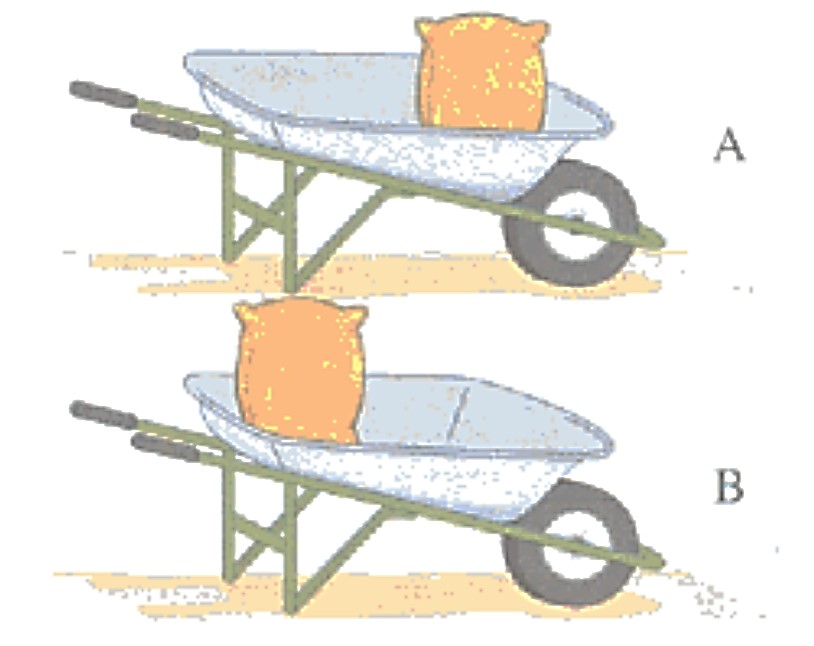
| Ejemplo:
¿Cuál es la manera más practica de cargar el saco en la carretilla? Razonamiento Mecánico: La manera más practica es la A, porque el saco esta más lejos de la persona que lleve la carretilla: en este caso la rueda está cumpliendo la Función de Roberto del ejemplo anterior. |
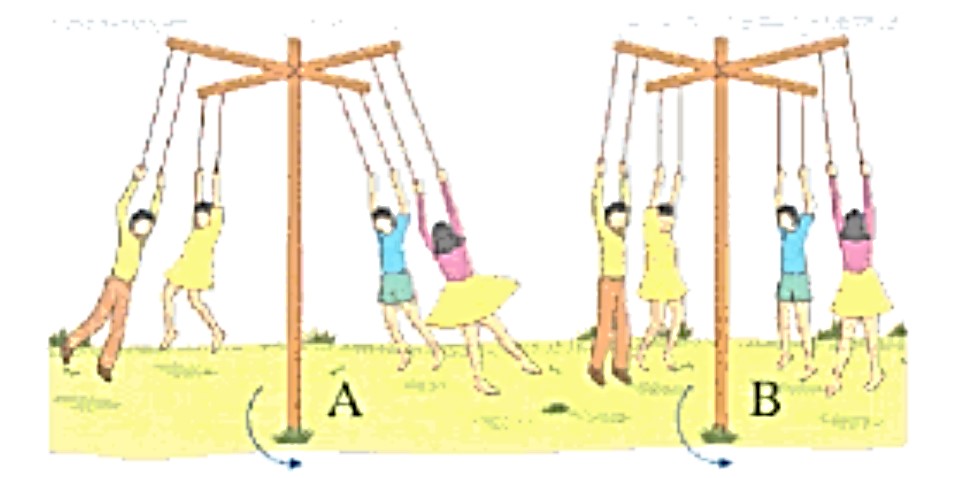
| Ejemplo:
¿Cuál de los grupos de niños se observa que está girando más rápido? Razonamiento Mecánico: El grupo de niños que está girando más rápido es el A, porque están más separados del poste, lo que demuestra que hay una mayor velocidad angular en esta situación. |
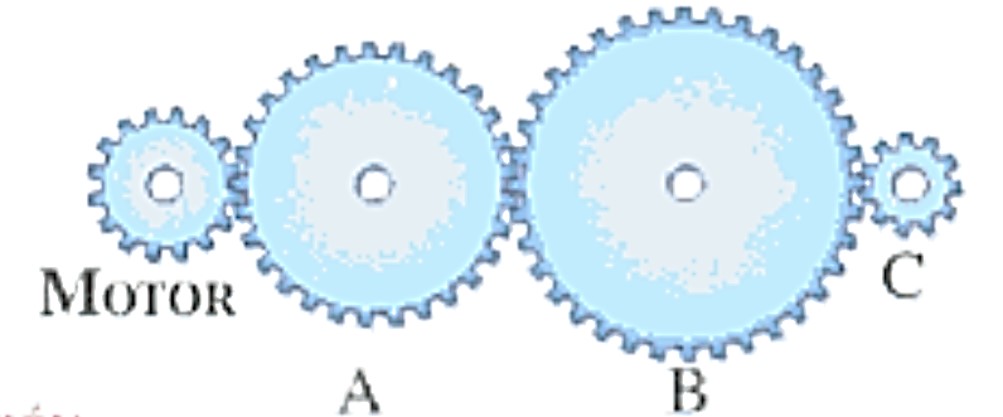
| Ejemplo:
En el sistema de engranajes mostrado ¿Cuál de las ruedas dentadas dará más revoluciones (giros) por minuto, si el engranaje motor es el que ocasiona el movimiento? Razonamiento Mecánico: La rueda dentada que dará más revoluciones por minuto es la C, porque es la más pequeña y tiene que realizar un mayor recorrido al tener menor número de dientes. Hay una relación inversa entre el número de dientes y el número de revoluciones. |
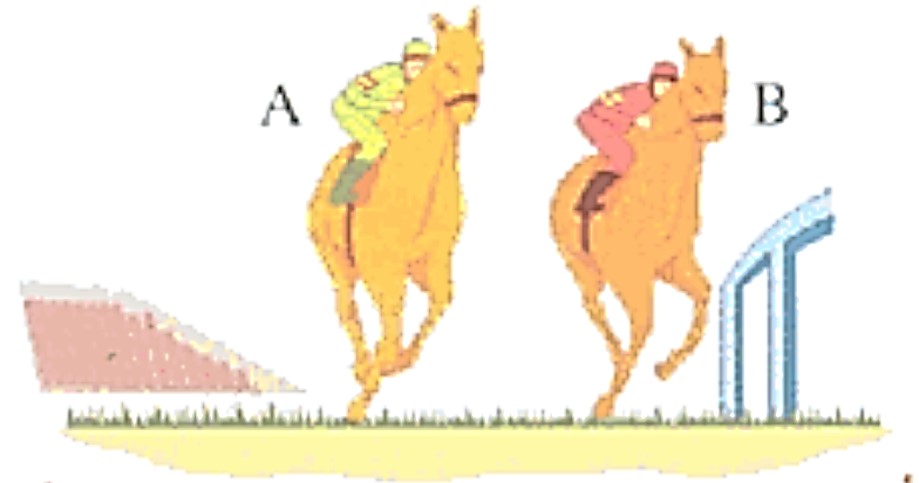
| Ejemplo:
¿Cuál de los caballos debe correr más rápido para mantener su lugar al dar la curva? Razonamiento Mecánico: El caballo A, porque debe correr una mayor longitud, mientras B está pegado a las barandas. |
Ejemplos de razonamientos mecánicos
DFL 1 Fija Texto Refundido, Coordinado y Sistematizado de la ley de tránsito
LEY 20.904 - Ley SRI Sistemas de Retención Infantil, aumento exigencias
LEY 20.770 - Ley Emilia, manejo en estado de ebriedad, causando lesiones
LEY 20.580 - Ley Tolerancia cero, manejo ebriedad-sustancias estupefacientes